This module implements an encoding of Presburger formulae. It computes also for a given formula its set of solutions using Shared Automata. More...

#include <ccl/ccl-log.h>
#include <ccl/ccl-hash.h>
#include <prestaf/prestaf-predicate.h>

Typedefs
typedef struct prestaf_formula_st	prestaf_formula
	Pointers to Presburger formula. More...

typedef struct prestaf_linear_term_st	prestaf_linear_term
	Pointers to linear terms. More...

Functions
ccl_list *	prestaf_formula_get_variables (prestaf_formula *f)
	Free variables of a formula. More...

prestaf_formula *	prestaf_formula_add_reference (prestaf_formula *f)
	Increments the reference counter of a formula. More...

void	prestaf_formula_del_reference (prestaf_formula *f)
	Decrements the reference counter of a a formula. More...

void	prestaf_formula_display (ccl_log_type log, prestaf_formula *f)
	Textual display of a Presburger formula. More...

prestaf_predicate *	prestaf_formula_solutions (prestaf_formula *f)
	Getting solutions of a Presbruger formula. More...

prestaf_formula *	prestaf_formula_create_or (prestaf_formula f1, prestaf_formula f2)
	Formulae disjunction. More...

prestaf_formula *	prestaf_formula_create_and (prestaf_formula f1, prestaf_formula f2)
	Formulae conjunction. More...

prestaf_formula *	prestaf_formula_create_equiv (prestaf_formula f1, prestaf_formula f2)
	Formulae equivalence. More...

prestaf_formula *	prestaf_formula_create_imply (prestaf_formula f1, prestaf_formula f2)
	Formulae implication. More...

prestaf_formula *	prestaf_formula_create_not (prestaf_formula *f)
	Formula negation. More...

prestaf_formula *	prestaf_formula_create_forall (ccl_list variables, prestaf_formula f)
	Universal quantification of a formula. More...

prestaf_formula *	prestaf_formula_create_exists (ccl_list variables, prestaf_formula f)
	Existential quantification of a formula. More...

prestaf_formula *	prestaf_formula_create_eq (prestaf_linear_term t1, prestaf_linear_term t2)
	Constructor for equality (==) of linear terms. More...

prestaf_formula *	prestaf_formula_create_neq (prestaf_linear_term t1, prestaf_linear_term t2)
	Constructor for disequality (!=) of linear terms. More...

prestaf_formula *	prestaf_formula_create_lt (prestaf_linear_term t1, prestaf_linear_term t2)
	Constructor for strict inferiority (<) of linear terms. More...

prestaf_formula *	prestaf_formula_create_leq (prestaf_linear_term t1, prestaf_linear_term t2)
	Constructor for large inferiority (<=) of linear terms. More...

prestaf_formula *	prestaf_formula_create_gt (prestaf_linear_term t1, prestaf_linear_term t2)
	Constructor for strict superiority (>) of linear terms. More...

prestaf_formula *	prestaf_formula_create_geq (prestaf_linear_term t1, prestaf_linear_term t2)
	Constructor for weak superiority (>=) of linear terms. More...

prestaf_linear_term *	prestaf_linear_term_create (uint32_t n, int a, ccl_ustring x, int b)
	Constructor for linear terms. More...

prestaf_linear_term *	prestaf_linear_term_plus (prestaf_linear_term t1, prestaf_linear_term t2)
	Add two linear terms. More...

prestaf_linear_term *	prestaf_linear_term_minus (prestaf_linear_term t1, prestaf_linear_term t2)
	Substract two linear terms. More...

prestaf_linear_term *	prestaf_linear_term_neg (prestaf_linear_term *t)
	Negate a linear term. More...

prestaf_linear_term *	prestaf_linear_term_add_reference (prestaf_linear_term *t)
	Increments the reference counter of a linear term. More...

void	prestaf_linear_term_del_reference (prestaf_linear_term *t)
	Decrements the reference counter of a linear term. More...

int	prestaf_linear_term_get_coef (prestaf_linear_term *t, ccl_ustring x)
	Getting coefficient of a linear term. More...

int	prestaf_linear_term_get_ith_coef (prestaf_linear_term *t, uint32_t i)
	Getting coefficient of a linear term. More...

void	prestaf_formula_statistics (prestaf_formula *F, ccl_log_type log)
	Display informations about the sataf_msa encoding the solutions of Presburger formula. More...

prestaf_formula *	prestaf_formula_linear_transform (prestaf_formula F, ccl_hash c, int a)
	Replace each free variables by . More...

Detailed Description

This module implements an encoding of Presburger formulae. It computes also for a given formula its set of solutions using Shared Automata.

Presburger formulae are syntactically defined by:

F ::= T == T | T != T | T < T | T <= T | T > T | T >= T | -F | F \/ F | F /\ F | F => F | F <=> F | E.x F | A.x F

E. and A. operators are respectively existential and universal quantification. T represents a linear term defined syntactically by:

T ::= c | a.x | T+T | T-T | -T

where c and a are an integers and x is a variable taken its value into natural numbers 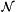$\cal N$ .

Definition in file prestaf-formula.h.

Typedef Documentation

typedef struct prestaf_formula_st prestaf_formula

Pointers to Presburger formula.

This type defines pointers to structures encoding Presburger formulae. These formula are syntactically defined by:

F ::= T == T | T != T | T < T | T <= T | T > T | T >= T | -F | F \/ F | F /\ F | F => F | F <=> F | E.x F | A.x F

E. and A. operators are respectively existential and universal quantification. T represents a linear term defined syntactically by:

T ::= c | a.x | T+T | T-T | -T

where c and a are an integers and x is a variable taken its value into natural numbers 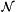$\cal N$ .

prestaf_formula uses a counter of references.

See Also: prestaf_linear_term

Definition at line 73 of file prestaf-formula.h.

typedef struct prestaf_linear_term_st prestaf_linear_term

Pointers to linear terms.

This type defines pointers to structures encoding linear terms of the form a₀.x₀+...+a_n.x_n+ b where a_i and b are integers and x_i are variables.

prestaf_linear_term uses a counter of references.

Definition at line 85 of file prestaf-formula.h.

Function Documentation

prestaf_formula* prestaf_formula_add_reference ( prestaf_formula * f )

Increments the reference counter of a formula.

Parameters

f	the formual to be referenced

Precondition: f != NULL toto

Returns: f

prestaf_formula* prestaf_formula_create_and	(	prestaf_formula *	f1,
		prestaf_formula *	f2
	)

Formulae conjunction.

Parameters

f1	first operand
f2	second operand

Precondition: f1 != NULL && f2 != NULL

Returns: a formulat encoding f1 /\ f2

prestaf_formula* prestaf_formula_create_eq	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Constructor for equality (==) of linear terms.

Parameters

t1	first operand
t2	second operand

Precondition: t1 != NULL && t2 != NULL

Returns: a prestaf_formula encoding t1 <= t2

prestaf_formula* prestaf_formula_create_equiv	(	prestaf_formula *	f1,
		prestaf_formula *	f2
	)

Formulae equivalence.

Parameters

f1	first operand
f2	second operand

Precondition: f1 != NULL && f2 != NULL

Returns: a formulat encoding f1 <=> f2

prestaf_formula* prestaf_formula_create_exists	(	ccl_list *	variables,
		prestaf_formula *	f
	)

Existential quantification of a formula.

Parameters

variables	the list of quantified variables
f	the formula to quantify

Precondition: variables != NULL && f != NULL; ccl_list_get_size (variables) > 0

Returns: A formula encoding E.x0 ... E.xn f where x0 ... xn are variables listed in variables.

prestaf_formula* prestaf_formula_create_forall	(	ccl_list *	variables,
		prestaf_formula *	f
	)

Universal quantification of a formula.

Parameters

variables	the list of quantified variables
f	the formula to quantify

Precondition: variables != NULL && f != NULL; ccl_list_get_size (variables) > 0

Returns: A formula encoding A.x0 ... A.xn f where x0 ... xn are variables listed in variables.

prestaf_formula* prestaf_formula_create_geq	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Constructor for weak superiority (>=) of linear terms.

Parameters

t1	first operand
t2	second operand

Precondition: t1 != NULL && t2 != NULL

Returns: a prestaf_formula encoding t1 >= t2

prestaf_formula* prestaf_formula_create_gt	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Constructor for strict superiority (>) of linear terms.

Parameters

t1	first operand
t2	second operand

Precondition: t1 != NULL && t2 != NULL

Returns: a prestaf_formula encoding t1 > t2

prestaf_formula* prestaf_formula_create_imply	(	prestaf_formula *	f1,
		prestaf_formula *	f2
	)

Formulae implication.

Parameters

f1	first operand
f2	second operand

Precondition: f1 != NULL && f2 != NULL

Returns: a formulat encoding f1 => f2

prestaf_formula* prestaf_formula_create_leq	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Constructor for large inferiority (<=) of linear terms.

Parameters

t1	first operand
t2	second operand

Precondition: t1 != NULL && t2 != NULL

Returns: a prestaf_formula encoding t1 <= t2

prestaf_formula* prestaf_formula_create_lt	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Constructor for strict inferiority (<) of linear terms.

Parameters

t1	first operand
t2	second operand

Precondition: t1 != NULL && t2 != NULL

Returns: a prestaf_formula encoding t1 < t2

prestaf_formula* prestaf_formula_create_neq	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Constructor for disequality (!=) of linear terms.

Parameters

t1	first operand
t2	second operand

Precondition: t1 != NULL && t2 != NULL

Returns: a prestaf_formula encoding t1 != t2

prestaf_formula* prestaf_formula_create_not ( prestaf_formula * f )

Formula negation.

Parameters

f	first operand

Precondition: f != NULL

Returns: a formulat encoding -f

prestaf_formula* prestaf_formula_create_or	(	prestaf_formula *	f1,
		prestaf_formula *	f2
	)

Formulae disjunction.

Parameters

f1	first operand
f2	second operand

Precondition: f1 != NULL && f2 != NULL

Returns: a formulat encoding f1 \/ f2

void prestaf_formula_del_reference ( prestaf_formula * f )

Decrements the reference counter of a a formula.

When the reference counter of the object falls to 0 then the memory allocated for the formula is released.

Parameters

f	the formula to be dereferenced

Precondition: f != NULL and there exists at least 1 reference to this formula.

void prestaf_formula_display	(	ccl_log_type	log,
		prestaf_formula *	f
	)

Textual display of a Presburger formula.

Parameters

f	the formula to be displayed

Precondition: f != NULL

ccl_list* prestaf_formula_get_variables ( prestaf_formula * f )

Free variables of a formula.

This function returns a list containing all the variables appearing in the given formula f.

Parameters

f	the formula

Precondition: f != NULL

Returns: The list of free variables appearing in the formula f. This list * has to be deleted by the client code.

prestaf_formula* prestaf_formula_linear_transform	(	prestaf_formula *	F,
		ccl_hash *	c,
		int	a
	)

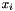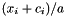Replace each free variables $x_i$ by $(x_i + c_i)/a$ .

Returns: a new formula

prestaf_predicate* prestaf_formula_solutions ( prestaf_formula * f )

Getting solutions of a Presbruger formula.

Precondition: f != NULL

Returns: a prestaf_predicate encoding the solutions of the formula f

void prestaf_formula_statistics	(	prestaf_formula *	F,
		ccl_log_type	log
	)

Display informations about the sataf_msa encoding the solutions of Presburger formula.

Parameters

F	a Presburger formula.
log	the log-stream where informations are displayed.

Precondition: F != NULL

prestaf_linear_term* prestaf_linear_term_add_reference ( prestaf_linear_term * t )

Increments the reference counter of a linear term.

Parameters

t	the term to be referenced

Precondition: t != NULL

Returns: t

prestaf_linear_term* prestaf_linear_term_create	(	uint32_t	n,
		int *	a,
		ccl_ustring *	x,
		int	b
	)

Constructor for linear terms.

This function allocates a structure encoding a linear term of the form a[0]*x[0]+...+a[n-1]*x[n-1]+b.

Parameters

n	the number of variables in this term.
a	the coefficient of each sub-term.
x	the names of variables.
b	the constant of the term?

Precondition: n >= 1 => (a != NULL && x != NULL)

Returns: A newly allocate linear term encoding a[0]*x[0]+...+a[n-1]*x[n-1]+b.

void prestaf_linear_term_del_reference ( prestaf_linear_term * t )

Decrements the reference counter of a linear term.

When the reference counter of the object falls to 0 then the memory allocated for the term is released.

Parameters

t	the term to be dereferenced

Precondition: t != NULL and there exists at least 1 reference to this term.

int prestaf_linear_term_get_coef	(	prestaf_linear_term *	t,
		ccl_ustring	x
	)

Getting coefficient of a linear term.

This function returns the coefficient of the variable x in t.

Parameters

t	the considered term.
x	the variable for which one want to get the coefficent..

Precondition: t != NULL && x != NULL

Returns: the coefficient of x in t; if x doesn't appear in t the function return 0.

int prestaf_linear_term_get_ith_coef	(	prestaf_linear_term *	t,
		uint32_t	i
	)

Getting coefficient of a linear term.

This function returns the i^th coefficient in t (the constant is not considered here). The subterms are ordered using the address of the variable names.

Parameters

t	the considered term.
i	the index for which one want to get the coefficent.

Precondition: t != NULL && i < the number of subterms

Returns: the i^th coefficient in t.

prestaf_linear_term* prestaf_linear_term_minus	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Substract two linear terms.

This operation computes the substraction of its two arguments. The set of variables of the two terms are merged before the operation.

Parameters

t1	the first linear term.
t2	the second linear term.

Precondition: t1 != NULL && t2 != NULL

Returns: t1 - t2

prestaf_linear_term* prestaf_linear_term_neg ( prestaf_linear_term * t )

Negate a linear term.

This operation negates its two arguments.

Parameters

t	the first linear term

Precondition: t != NULL

Returns: - t

prestaf_linear_term* prestaf_linear_term_plus	(	prestaf_linear_term *	t1,
		prestaf_linear_term *	t2
	)

Add two linear terms.

This operation computes the sum of its two arguments. The set of variables of the two terms are merged before the operation.

Parameters

t1	the first linear term
t2	the second linear term

Precondition: t1 != NULL && t2 != NULL

Returns: t1 + t2

Typedefs

Functions

Detailed Description

Typedef Documentation

Function Documentation